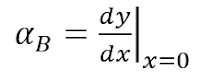Slope and Deflection in Beams

Beams

A beam is a structural element that primarily resists loads applied laterally to the beam's axis. Its mode of deflection is primarily by bending. The total effect of all the forces acting on the beam is to produce shear forces and bending moments within the beam, that in turn induce internal stresses, strains and deflections in the beam. Beams are characterized by their manner of support, shape of cross-section, equilibrium conditions, length, and their material.

Beams were traditionally descriptions of building or civil engineering structural elements, but any structure such as automotive automobile frames, aircraft components, machine frames, and other mechanical or structural systems contain beam structures that are designed to carry lateral loads are analysed in a similar fashion.

Beams are mainly classified on the basis of their supports:
Simply supported beam, which is supported on the ends which are free to rotate and have no moment resistance. 
Cantilever beam, which is a projecting beam fixed only at one end. 
Over hanging beam, which extends beyond its support on one or both ends. 
Fixed beam, which is supported on both ends and restrained from rotation. 
Continuous beam, which extends over more than two supports. 

Basic three types of loads act on these beams viz. Point load, Uniformly Distributed Load i.e. UDL, Uniformly Varying Load i.e. UVL.
    

      Slope and Deflection

      Beams when under action of any of these loads produce some deflection and slope at the ends. Slope of a beam is the angle between deflected beam to the actual beam at the same point and deflection is defined as the vertical displacement of a point on a loaded beam. Beams can vary greatly in their geometry and composition. For instance, a beam may be straight or curved. It may be of constant cross section, or it may taper. It may be made entirely of the same material i.e. homogeneous, or it may be composed of different materials i.e.  composite. Some of these things make analysis difficult, but many engineering applications involve cases that are not so complicated. Analysis is simplified if:

1.       The beam is originally straight and taper (if any) is slight.
2.       The beam experiences only linear elastic deformation.
3.       Length to height ratio of the beam is greater than 10.
4.       Only small deflections are considered (maximum deflection less than 1/10 of span).   

The maximum deflection occurs where slope is zero.  The position of the maximum deflection is found out by equating the slope equation zero.  Then the value of x is substituted in the deflection equation to calculate the maximum deflection. 

There are many methods to find out the slope and deflection at a section in a loaded beam.

• Double Integration method

This is most suitable when concentrated load or UDL over entire length is acting on the beam. The double integration method is a powerful tool in solving deflection and slope of a beam at any point because we will be able to get the equation of the elastic curve.

    

where, M=bending moment, I=area moment of inertia of section of the beam, y=deflection in the beam, E=modulus of elasticity of beam material

Integrating twice, we get the following equation                                                                                                                                                                                                                                                                   

Hence, deflection in the beam can be given as:          

Also, the equation can be solved for deriving the slope at the ends using boundary conditions for the respective beams. Slope is given by:

• Area moment method

Another method of determining the slopes and deflections in beams is the area-moment method, which involves the area of the bending moment diagram. The moment-area method is a semi-graphical procedure that utilizes the properties of the area under the bending moment diagram. It is the quickest way to compute the deflection at a specific location if the bending moment diagram has a simple shape. Using Mohr’s theorems, slope and deflection can be calculated for various beams using the bending moment diagram.

1. Mohr's theorem for slope

where α=slope, A=area under bending moment diagram, E=modulus of elasticity, I=area moment of inertia.

     2.  Mohr's theorem for deflection

where y=deflection in beam, x=x of bending moment diagram, E=modulus of elasticity, I=area moment of inertia

• Method of Superposition

The method of superposition, in which the applied loading is represented as a series of simple loads for which deflection formulas are available. Then the desired deflection is computed by adding the contributions of the component loads(principle of superposition).

Slope and deflection formulae for a cantilever beam

Slope and deflection formulae for a simply supported beam

The purpose of calculating deflection in beam is to determine the vertical depth of its sag from initial horizontal (longitudinal) axis of beam. And the slope is the angle of beam axis between initial position and final position after deflection. Some important factors also depend on the deflection in beam:

1. Deflection of beam controls the effective length to depth ratio of beam.
2. Sometimes deflection does not affect the structural stability but due to excessive deflection, minor cracks may develop in structures like in plaster etc. which are not good from the appearance point of view. Therefore, to avoid cracks, deflection should be within the permissible limit.

         Calculating slope deflection gives us theoretical representation of beam after the application of load. Deflection gives us the value to which the beam will deflect after the application of load. Whereas Slope defines how the beam is going to deflect after application of load (shape of bend/deflection). So the reason behind calculating slope and deflection is to know how the beam will bend and to which extent. Except the design purpose, the slope and deflection helps us get to know how the beam will behave after load application and decide its position relatively to other members according to the behavior of beam. It also helps in deciding other architectural designs.

Group members:

1. Maanas Sindkar      (C-21, 11810273)             
2. Saurabh Solanke     (C-22, 11810466)
3. Anuj Sonawane       (C-23, 11810837)
4. Atharva Sule            (C-24, 11810483)